Two Dimensional Diffusion Equation.
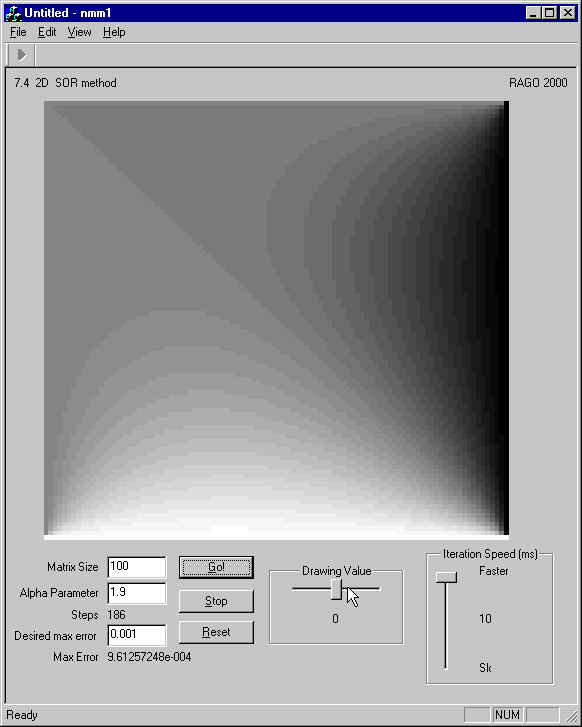
The software uses the Successive Over - Relaxation (SOR) method to update a matrix. This matrix can be thought as the electric potential in a square area, or the temperature gradient in a room. This particular implementation has Fixed boundary conditions.
The parameter alpha determines the ammount of "overshooting" that the algorithm will do every iteration. A very big alpha (greater than 2) will make the algoritm totally unstable. alphas between 1 and 2 will make the algoritm to oscillate when it gets closer to the answer, but it will converge faster.
The Desired error parameter will determine the threshold for the termination criteria (when the measured error is below the desired error)
About the Software:
Compiled in VC++ 6.0, Win NT 4.0 using MFC.
Download the software 2DDiffexe.zip 149 KB or 2DDiff.exe 300 KB
Download the VC project 2DDiff.zip 51 KB
Usage:
Select a Matrix size (maximum 500,) for the square matrix. The matrix can hold float
values ranging from -1 to 1. (i.e. -1 = cold, 1 = hot, or -1 = negative potential, 1=
positive potential). The default matrix has two walls filled with zeroes, one with 1's and
one with -1's. The values at the walls are fixed during the whole simulation (the program
never changes them) but the user can change them when drawing new values.
To start the simulation press "Go!". The speed can be changed using the scroll control.
To draw new values, select the "drawing value" moving the horizonal scroll control (the value to be drawn is shown below) and use the mouse and the left button to draw over the image. The values drawn on the walls (or boundaries) will not be changed by the algorithm.
The desired error will be the threshold for the maximum error allowed. When the computed error falls below it, the iteration stop.